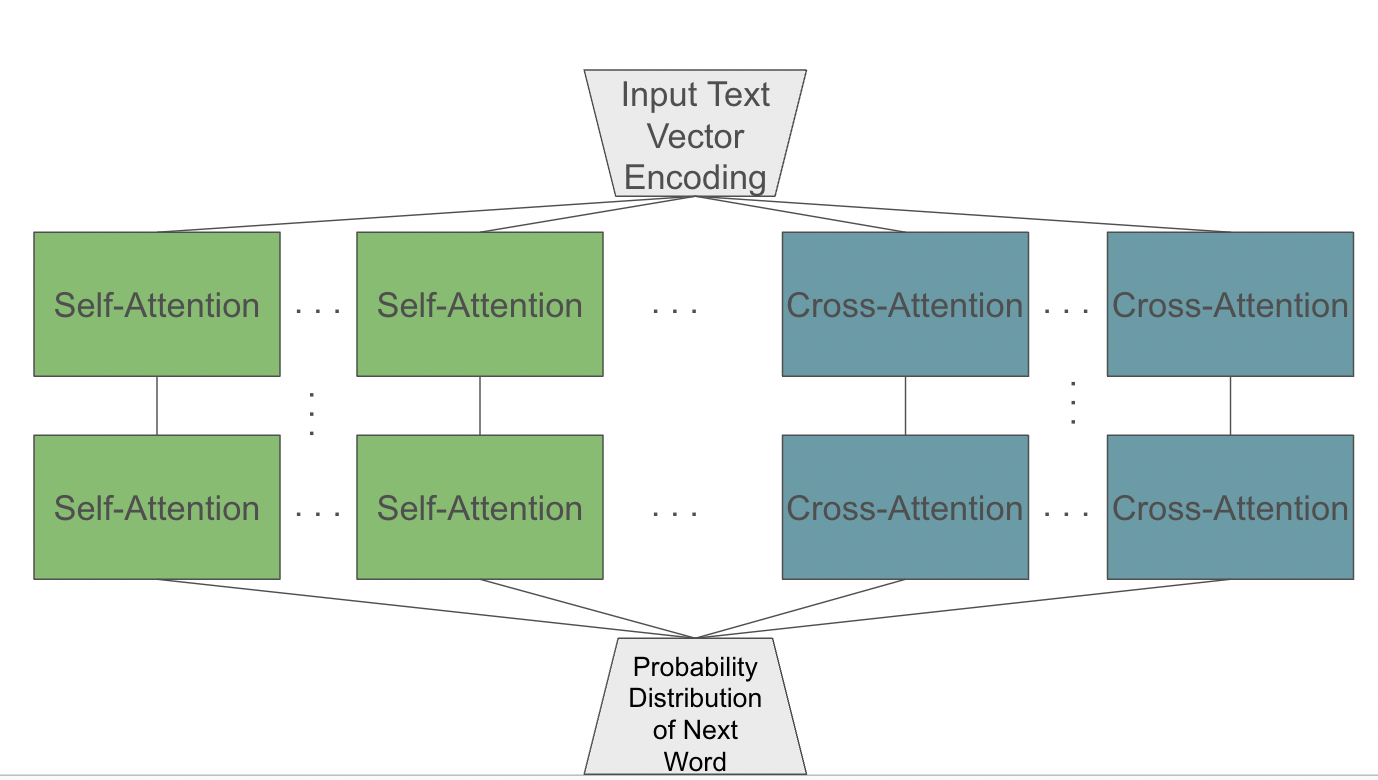
Transformers and Positional Encoding

Written by Francis Cataldo and Thomas Normand

Motivation

Given the example sentence: the cow jumped over the moon. Convert the sentence into an nxd tensor (n is the number of words, d is the vector length) where each words is one-hot encoded into a vector.

Another example sentence: the cat plays the fiddle

Convert the sentence into an mxd tensor (m is the number of words, d is vector length). Now, we want the following: takes sequences of varying lengths, accounts for short range and long range dependencies, and considers context of words (i.e. fiddle with door vs. fiddle the instrument).

Attention is the solution… We will consider two versions of attention: Self-Attention and Cross-Attention

Self-Attention

The self-attention layer takes in one-hot encodings of words and returns a linear combination of the inputted vectors

Note: the subsequent stacked layers take in linear combinations of vectors and return probability distributions

At the end, the vectors are passed into another trained aspect of the model that takes in the linear combination of vectors from the previous attention layers and returns a probability distribution of the next word

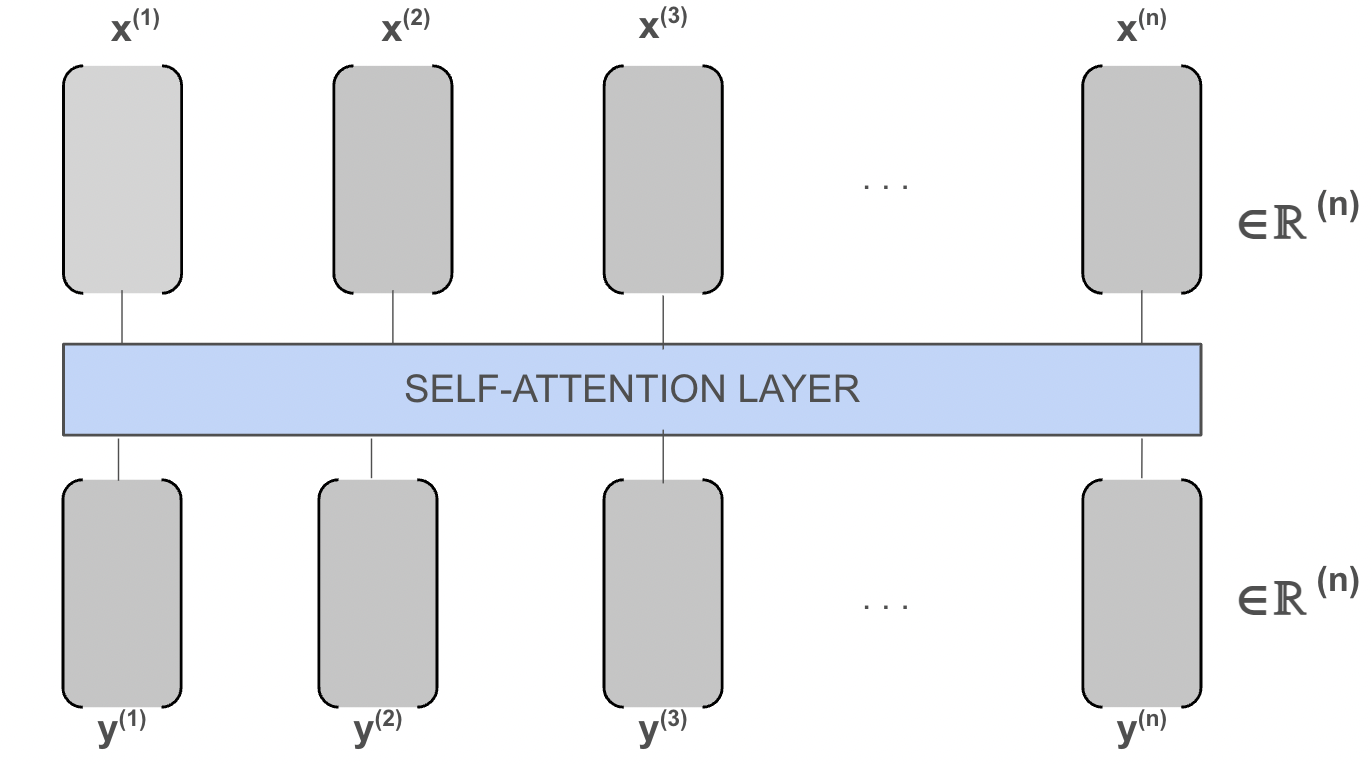
This model is implemented via matrix multiplications simplified into the following diagram.

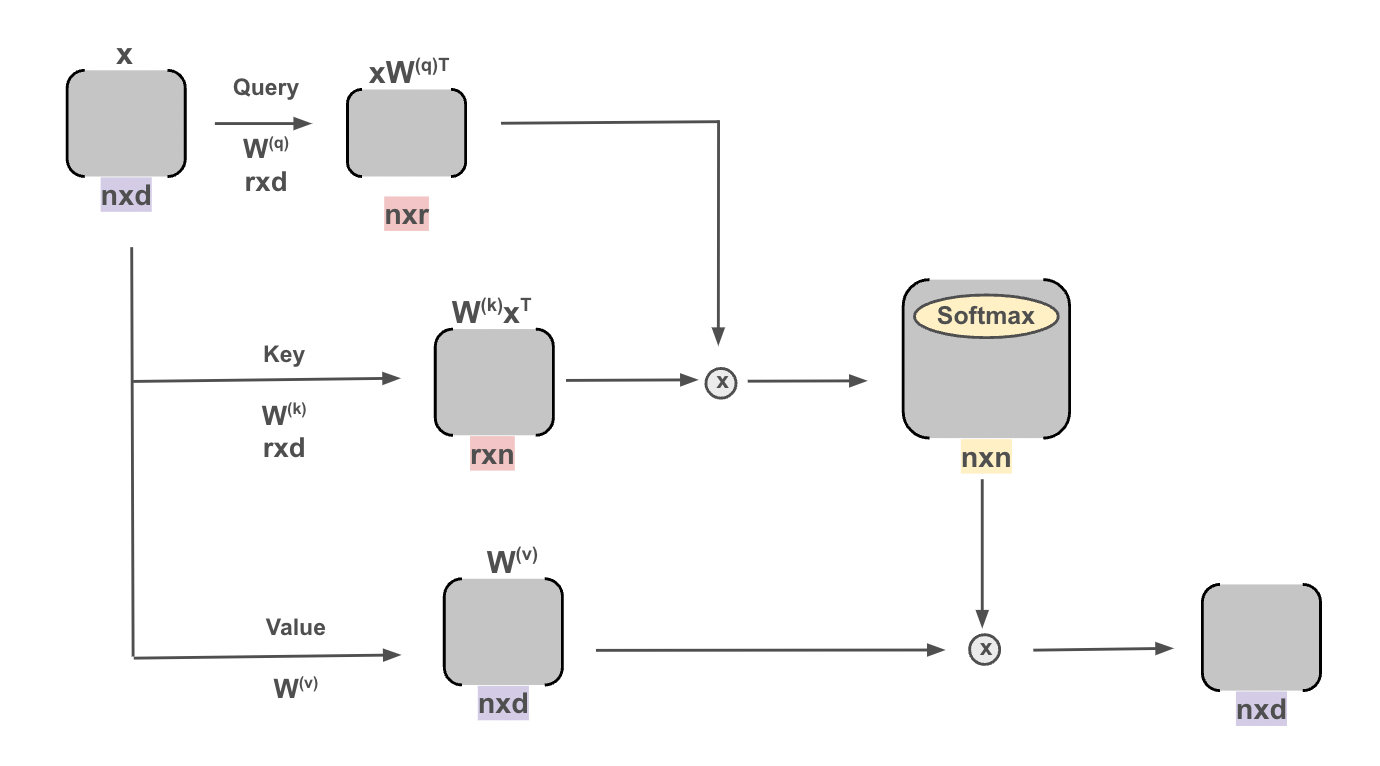
Here, the “W” matrices are simply trained weights and the “X” matrix is the inputted words. The “X” matrix is broken up into queries, keys, and values that are run through the matrix multiplications. After, they are passed through the softmax to create a probability distribution

We begin by establishing that each predicted vector \(y^{(i)}\) should be a linear combination of the other words in the vocabulary. That is, \(y^{(i)}=\sum_{i=1}^n x^{i}\text{sim}(i,j)\) One way to calculate the similarity between the ith and jth words is softmax. However, we aren’t fully leveraging the power of deep learning. Note that since attention models are fully connected, they can be thought of in terms of matrix multiplication. This motivates a modified approach.

Incorporating a weight matrix \(W^{(v)}\) we write,

\(y^{(i)}=\sum_{i=1}^n W^{(v)}x^{i}\text{soft}(<W^{(k)}x^{(i)},W^{(q)}x^{(j)}>)\) \(\Rightarrow W^{(v)}\sum_{i=1}^n x^{i}\text{soft}(x^{(i)^T}W^{(k)^T}W^{(q)}x^{(j)})\)

We’ve encountered an issue: computing the outputs in this way is extremely time consuming. How can we refine this approach?

Let \(X\) be the matrix containing the vector embeddings of each word and consider the \(W^{(q)}x^{(j)}\) term. Note that by indexing the jth row of the resulting matrix of \(XW^{(q)^T}\) we obtain \(W^{(q)}x^{(j)}\). Similarly, if we index the jth column of \((XW^{(k)^T})^T\) we can find \(W^{(k)}x^{(i)}\). Then, because softmax produces a vector, call it \(v^{(i)}\), we can rewrite this as,

\(W^{(v)}\sum_{i=1}^n x^{i}\text{soft}(x^{(i)^T}W^{(k)^T}W^{(q)}x^{(j)})\) \(\Rightarrow \text{soft}(XW^{(q)^T}W^{(k)^T}X)XW^{(v)}\)

We now have a succinct way of representing the desired outputs in terms of matrix multiplication, a task modern GPUs are very good at. By indexing the jth row of this resulting matrix, we can obtain \(y^{(j)}\).

Self-attention got its name because the queries and keys are the same
Self-attention layers are stacked on top of each other
1. Some models use as many as 96 layers in sequence. Also possible to utilize them with multiple self-attentions in one layer.
At the end, a sequence of vectors is returned that can be interpreted as a probability distribution of the next word.
Next, the value should be interpreted as a probability. Training is required to improve this.
This process is achieved by repeatedly testing the model against known text with select words removed. The model then predicts the word and is evaluated via the cross entropy loss function and then, the weights are updated.

Cross-Attention

Modivation: Cross-Attention allows for the translation of meaning between languages. It differs from Self-Attention because Cross-Attention analyzes the connections between two sequences and Self-Attention analyzes only one sequence.

In implementation, Cross-Attention is very similar to Self-Attention with the small tweaks highlighted on the following diagram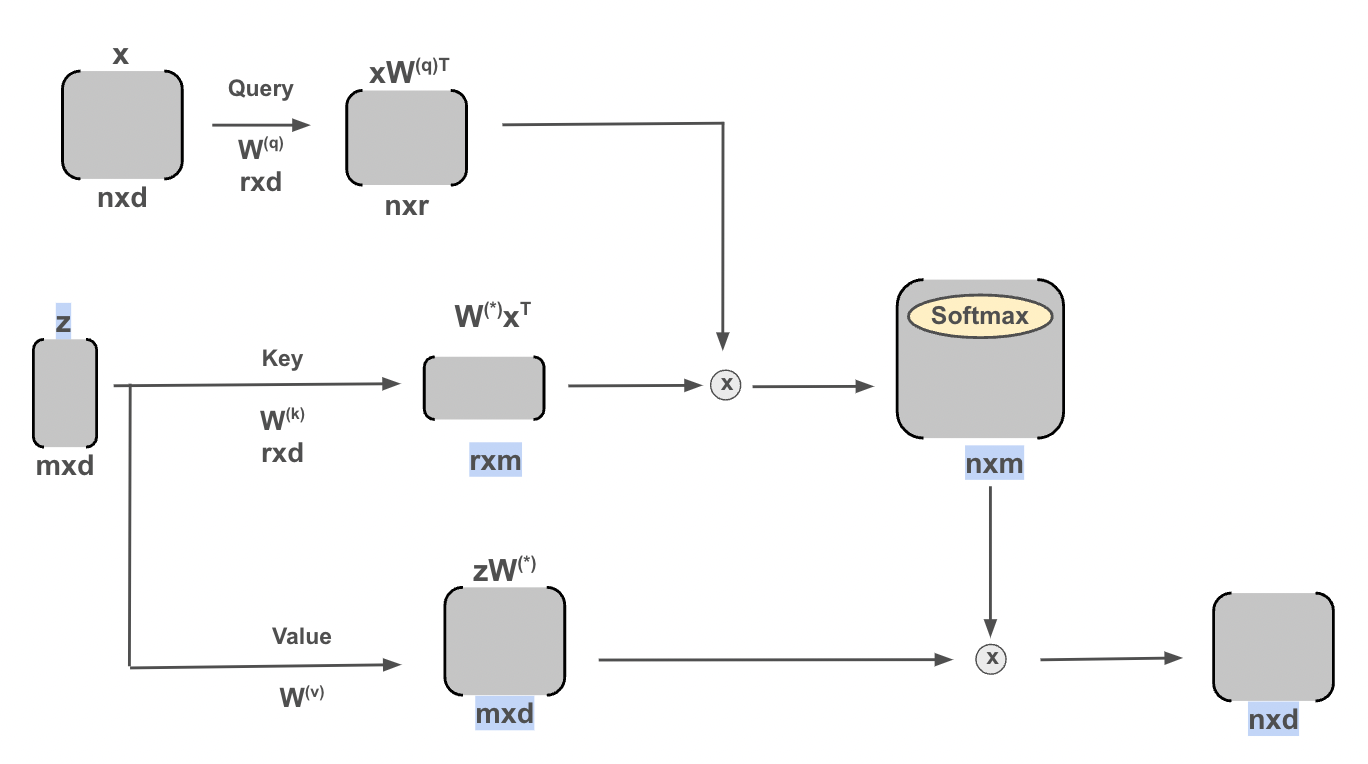

Positional Encoding

Modivation: Consider the time representation 1,065,066,880 minutes since 0 BC. This is not easily understandable. In practice, instead of this, we encode this time as 11:24am Tuesday, Jan 14, 2025. This is an example of positional encoding. The minute, day, and date are all useful for scheduling. The hour attribute captures the time of day, month captures the time of year, and year counts the years past.

A certain time can be encoded by drawing a line from through the different sinusodial fucntions, like the red line shown above. These values can be thought of as the result of different sinusodial functions. All of this culminates to a much more readable value. This concept will be utilized in machine learning by encoding strings in a similar manner in a subsequent lecture.

In practice, we add on this new information to the bottom of each of the one-hot encoded vectors and access it later to retrieve the positional information. In true LLMs, self-attention and cross attention layers are implemented in series and in parallel, each focusing on different elements of the input text.